在公务员备考过程当中，关于比较大小这种题型，考生知道可以用观察比较的方式，也可以利用比较增长率的方式。但是经过实际做题大家会发现，有些题目，用这两种方法都很难比较出来。中公教育专家今天给大家介绍一种新的方法，叫做差分比较法。差分比较法就是基于同位比较基础之上的一种延伸，能够一定程度解决上述问题。

首先我们来看看什么情况下，我们会采取这种方式来进行比较。

我们来看一个例子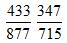，。拿到这两个数之后，我们首先应该想到的是能不能通过观察解决，那么我们可以看到433的2倍是866，略小于分母877.所以这是个略小于50%的分数。另外一个，347的2倍是694，同样略小于分母。所以后面这个也是略小于50%的，那么通过观察，我们无法比较出大小。

其次我们再用同位比较法来尝试，先看两个分子，347与433相差了86，用错位加减法来衡量，相当于34的2倍还多一些。再看分母，715和877相差了162，也相当于71的2倍还多。此时分子分母具体变化的幅度哪个大仍然是不好观察。所以对于这类题目，就要用到今天所学的差分比较法。

先来看一下我怎么操作:(简单求解)

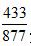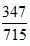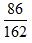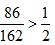将写在中间，写在一边，用433-347得到86，用877-715得到162，这样就得到了一个新的分数，观察可知，比较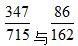的大小，发现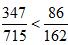，即可得到。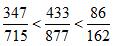

为什么能得到这个结论呢?这就需要了解差分比较法的原理。

接着我们来看看差分比较法的原理。

我们先观察刚才的两个分数，会发现分子分母这四个数字都大于0，而且还存在着第一个分数的分子分母同时大于后一个分数的分子分母。也就是433大于347,877大于715，在这里我们要注意到分子分母大小关系同向，因为如果异向，就可以通过观察得出结果。那么针对于这种形式的题目，我们首先要把分子分母较大的分数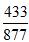写在中间，分子分母较小的分数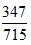写在一边;然后将分子分母同时做差，大的减小的，分子之差做分子，分母之差做分母得到一个新分数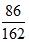，写在另一边;这样我们就有了3个分数。

在这三个分数之中，大小关系是怎样的呢?我们用数量当中溶液的模型来分析。

现在假设有两瓶溶液，第一瓶当中有溶质347克，溶液715克。那么该溶液的浓度就是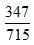。另外一瓶有溶质86克，溶液162克。那么该溶液的浓度就是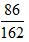。现在把这两瓶溶液混在一起，溶质就变成了347+86=433克，溶液就变成715+162=877克。那么混合而成的新溶液浓度就变成了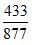。我们都知道两种不同浓度的溶液，混在一起之后，形成新溶液的浓度一定介于原来的两者之间。所以这三个分数大小关系中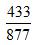，一定是最中间的。

之后，我们可以用新分数与分子分母较小的分数做比较来确定三者关系，因为两者差距比较大，相对容易比较。(但是也有例外情况，比如新分数和分子分母较大的分数的分子或分母某个位置相近，但另外一个位置相差较大，比较起来非常明显的时候，也可以让这两个做比较来确定三者关系。)那么我们应用这一点，用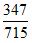和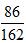比较，很明显前者小于50%,后者大于50%。那么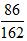就是三者之中最大的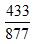，在中间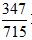，就是三者之中最小。

在这里我们要注意到我们做题的第一个步骤是把分子分母较大的分数写在中间，分子分母较小的分数写在一边;第二个步骤是将分子分母同时做差得到一个新分数，新分数写在另一边，保证分子分母较大的分数永远在中间;第三个步骤是用新分数和分子分母较小的分数做比较，确定三者关系。这在三个数中，不等号永远同向。

最后，在使用时有哪些需要注意的地方。

刚才我们学习了方法，原理以及解题步骤，并且解决了刚才的题目。但我们在做题的时候，偶尔会碰到一次差分解决不了的问题，这时就涉及到了多次差分。比如我们来看这两个分数： 。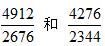

首先观察一下这两个分数，都略小于2，不能通过观察区分。再看相同位置变化，4276到4912增加了636，相当于4276增长了百分之十几;分母2344到2676增加了332，同样相当于2344增长百分之十几，分子分母扩大的幅度差不多，仍然不好判断。

我们把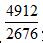写在中间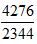，写在一边，分子分母同时作差得到了一个新的分数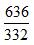，保证分子分母较大的分数 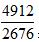始终在中间。通过观察可以看到，新分数也略小于2，同样不好判断它与分子分母较小的分数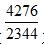之间的大小关系。那么这个时候，就把题目转化为 与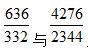之间的比较。此时可以继续使用差分法，但是由于这两个分数相同位置数字差距过大，作差后得到的分数，分子分母数字也会较大。我们都知道数字越小越容易判断大小关系。所以为了避免作差后数字过大，我们将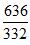分子分母同时扩大相同的倍数，以方便比较。在这里为了方便计算，我们把分子分母同时扩大10倍变成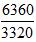。分子分母同时作差得到了一个新的分数。

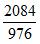列式如下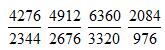，。此时比较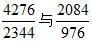 ，通过观察即可得知 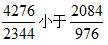。所以这几个数字之间大小关系可以确定即。

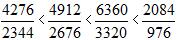通过这个题目，我们可以看到，在一次差分不能解决的题目当中，我们可以通过多次差分，继续扩大差距来解决。在多次差分的过程中，很多时候需要比较新分数和分子分母较小的分数之间的大小关系。如果相同位置数字差距较大，可以将某一个数字分子分母扩大相同的倍数，在保证其大小关系不变的前提下，方便我们继续差分比较。并且多次差分的过程中，为了保持不等号始终方向一致，需要始终保持分子分母较大的分数在中间，分子分母较小的分数与新分数各在两边。

首先回忆做题的过程，刚才都是差分之后，通过观察或者同位比较的方式最终来解决问题。所以差分是手段，是过程，不是最终目的，最终仍然要使用观察或者同位比较的方法。其次，我们再看同位比较与差分一样，都是相同的位置做比较，同位比较比的是变化幅度，算的是乘除法关系。差分是通过相同位置作差得到新分数后，用新分数和另外的分子分母较小的分数做比较，在这时我们既可以横向相同位置比较，也可以纵向通过观察的方式比较。也就是说差分法在同位比较的基础之上，增加了比较维度。最后，我们可以看到，差分法可以多次作差甚至无限作差，通过这种方式扩大分数之间的差距，最终成为可以通过观察比较出大小关系的题目。

相关文章：

2018国家公务员面试时间_面试公告通知汇总（湖南地区）

2018国考查排名看分差 国面轻松逆袭

相关阅读：