排列组合一直是令很多考生头疼的题型,其缘由一般来源于两个方面:其一是对于排列组合概念的理解不够深刻,在解题的时候容易错用排列数和组合数,其二是计算过程中思维不够严谨,导致计算的时候或计算重复,或计算漏数。针对这两种常见错误,我们都得学会牢固掌握几个学习步骤,中公教育专家在此以同素分堆模型为代表来演示一下,对于排列组合应该如何避免犯错误。
一、模型特征
要运用排列组合的任何一个公式都应该先熟悉它所描述的模型特征。那么,什么叫同素分堆呢?简单来说就是把相同的多个元素,按要求分成不同的份数,每份可能有独立的要求。例如:把10颗相同的糖分给4个小朋友,有多少种分配方式?把20个优秀班干部分给三个班,要求一班至少3个,二班至少4个,三班至少5个。这些都叫做同素分堆问题。特征的核心在于相同元素的分堆问题
二、公式推导
为了更好的理解同素分堆模型,接下来我们详细的把同素分堆的公式进行一个系统的分析和总结,帮助各位考生去理解和运用。
例:把10颗相同的糖果分给3个小朋友,每人至少分一颗,请问有几种不同的分法?
理解这句话本身不难,我们也可以适当的写出一部分10=1+1+8=1+2+7+……,很显然,如果完全依赖于枚举的话肯定会非常的麻烦,因此,我们需要简化这个模型:
首先,我们知道如果把一根木棒锯成三段,只需要两次,那么我们就可以把10颗球简化成一条线:要把10颗球分给三个小朋友,等价于把这根木棒分成三段,也就是在这10个球中插入两根木棒就可以了,而在插入木棒的时候,因为每堆至少分一颗,所以两边是不可以插板子的,并且同一个位置只能插入一根板子。
这种方法就可以分出3+6+1的结论,因此,最终的结果就是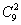 。
。
公式:n个相同的元素分成m堆(n>m),每堆至少分一个,那么所有的种类是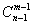 。
。
责任编辑(hnoffcn_zyq)